Abstract : Measurement uncertainty is very important in the inspection work. ISO and other international organizations have already requested it. This paper analyzes the error sources of ultrasonic wave detection longitudinal wave detection and evaluates the uncertainty during the flaw detection process.
Key words : ultrasonic flaw detection longitudinal wave method measurement uncertainty analysis
CLC number : TB553
Foreword
Measurement uncertainty (referred to as uncertainty) is used to characterize the dispersion of reasonable measurement values. It is an important parameter to evaluate measurement results [1 , 2] , which is the correct evaluation and use of standardized measurement results, international standardization, etc. In 1993, the organization jointly developed the "Guidelines for the Expression of Measurement Uncertainty" and applied it widely. In 1996, the domestic uncertainty in the measurement and verification work began to be promoted, but it is not widely used in the quantitative analysis of non-destructive testing. In order to facilitate international integration, this paper applies uncertainty to non-destructive testing and discusses it with you.
The error of longitudinal wave flaw detection comes from the flaw detector, probe, test block, workpiece, coupling agent, etc. There are measurement uncertainties in the process of defect location measurement and quantitative analysis. The evaluation uncertainty can indicate the results of flaw detection analysis. Reliability, has a good promotion value.
1 Location of defects
The longitudinal wave scanning speed is adjusted by 1:n, and the horizontal scale value of the front edge of the defect wave is Ï„ f , and the distance from the defect to the probe is [3] :
X f =nτ f
(1)
1.1 Instruments, workpieces
(1) EPOCH-II ultrasonic flaw detector; (2) 2.25P0.75' probe; (3) CSK-I test block; (4) workpiece with a thickness of 100 mm.
1.2 Determination of position
The instrument adjusts the scanning speed by 1:1, the horizontal scale value is 69.64, and the defect position:
X f =nτ f =69.64 mm
1.3 Uncertainty evaluation
(1) Adjusting the uncertainty caused by the scanning speed When the scanning speed is adjusted, a reading error due to the minimum scale limit of the display screen is generated. The minimum level of the instrument used is 0.1, and the reading can reach the minimum scale of 1/10, that is, the reading error distribution range is (-1/10, +1/10) scale, which is uniform distribution, standard uncertainty (with relative uncertainty) Representation) [4] : 
; its unreliability is 50%, degree of freedom v 1 = 
(50%) -2 = 2
(2) The level affects the horizontal linearity of the instrument affecting the positioning accuracy of the defect. The horizontal linearity of the instrument is 5.7×10 -3 , subject to the normal distribution (k=3), and its standard uncertainty: 
(Class B): its value is reliable, the degree of freedom v 2 =∞
The horizontal scale error is affected by the resolution of the instrument (resolution 0.01), subject to uniform distribution, the error is 1/2 resolution, the distribution range (-0.005, +0.005) [5] , its standard uncertainty (relatively uncertain) Degree representation): 
; (Class B); reading reliability is 50%, degree of freedom v 3 = (50%) -2 = 2
The horizontal scale values ​​were measured 10 times, with an average of 69.64 and a standard deviation of s=0.21. The standard uncertainty (represented by relative certainty): 
; (Class A): Degree of freedom v 4 = n-1 = 9
The horizontal scale synthesis standard uncertainty is the synthesis of the three standard uncertainties of the instrument's horizontal linearity, instrument resolution, and horizontal scale value repeated observation, which is the synthesis of the above three Class A and Class B:
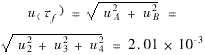
(3) The results are used to evaluate the transfer function of each component: 
=n=1
The location of the defect, its synthetic uncertainty:
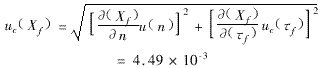
Effective degrees of freedom:
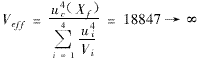
Take the confidence level 95%, t P (0.95)=1.96
The defect position is: X f (1±t P u C (X f ))=69.64 (1±8.8×10 -3 )
Its absolute uncertainty (synthetic standard) u C (X f )=X f . u C (X f )=0.3127
2 Quantitative analysis of defects
The defect equivalent size is calculated by the following formula:
(2)
It can be seen from the formula (2) that the defect equivalent size is affected by the defect position, the thickness of the workpiece, and the amount of attenuation.
2.1 Change in attenuation
The variation in attenuation during detection is caused by vertical linearity, probe frequency, attenuator error, couplant, medium attenuation, and the like.
2.1.1 The effect of vertical linearity is obtained by the following equation: vertical linearity and attenuation:
(3)
Where: H 0 —— ideal wave height H 1 —— measured wave height (H 1 1 is replaced by H 1 1 for one measured wave height, H′′ 1 is substituted for H 1 for the second measured wave height)
1 wave height effect transfer function 
×0.4342944=10.9
The linearity error is 4.7×10 -2 , subject to a normal distribution (k=3), and the standard uncertainty (represented by relative uncertainty): 
(Class B); its value is stable, and the degree of freedom v 5 =∞.
The reading error is 1/2 of the resolution, subject to a uniform distribution range (-0.5, +0.5), and standard uncertainty (expressed in relative uncertainty): 
; (Class B) its estimated reliability is 50%, degree of freedom v 6 = (50%) -2 = 2
The uncertainty of a wave height is synthesized by the above two types of Class A and Class B, namely:
10 -2
2 secondary wave height effect transfer function 
The second wave height has a linearity error of 4.7×10 -2 , and its standard uncertainty is:
u 7 =u 5 =1.57×10 -2 (Class B); degrees of freedom v 7 =v 5 =∞
The reading error is the same wave, u 8 =u 6 , v 8 =v 6
The uncertainty caused by the linear error is the synthesis of the primary wave height and the second wave height standard uncertainty, namely:
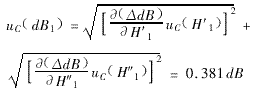
2.1.2 Effect of frequency-induced attenuation frequency on attenuation: 
Transfer Function: 
Frequency error 10%, subject to normal distribution (k=3), standard uncertainty: 
; its value is stable, the degree of freedom v 9 =∞
Standard uncertainty that causes attenuation:
2.1.2 Influence of coupling agent
Change the thickness of the coupling agent, measure its attenuation, and analyze its uncertainty by statistical method (the number of times of this test is 10). The average value of the test is 5.5 dB, the standard deviation is s=0.566, and the standard uncertainty is:
Expressed in relative uncertainty: 
10 -2 ; degrees of freedom v 10 = 10-1=9
The error caused by the reading is 1/2 of the resolution, subject to uniform distribution, and its distribution range is (-0.05, +0.05), standard uncertainty:
Expressed in relative uncertainty: 
; reading reliability 50%, degree of freedom v 11 = (50%) -2 = 2
Effect of attenuator accuracy (measured at 12dB):
Attenuator error 0.5dB, subject to normal distribution (k=3), standard uncertainty:
Expressed in relative uncertainty 
10 -2 ; its value is stable, and the degree of freedom v 12 =∞.
The uncertainty of the amount of attenuation caused by the couplant is the synthesis of the above three Class A and Class B:
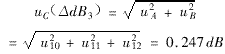
2.1.4 Media attenuation Repeat inspection of the workpiece (10 times), the medium attenuation, the mean value is 5.3, the standard deviation s=0.2 dB, the standard uncertainty is determined:
Expressed in relative uncertainty: 
;degree of freedom v 13 =10-1=9
Standard uncertainty due to reading: u' 14 = u 11 = 0.029 dB (Class B)
Expressed in relative uncertainty: 
10 -3 ; degrees of freedom v 14 =v 11 =2
Effect of the attenuator: u 15 =u 12 =0.167 dB (Class B)
Expressed in relative uncertainty: 
×10 -2 ; degree of freedom v 15 =v 12 =∞.
The uncertainty of medium attenuation is the synthesis of the above three Class A and Class B: 
2.1.5 Attenuation Amount Changes of repeated observations The workpiece is measured 10 times, with an average of 6.2 and a standard deviation of s=0.58. The standard uncertainty is:
Expressed in relative uncertainty: 
;degree of freedom v 16 =10-1=9
Standard uncertainty due to reading error: u 17 =u 11 =0.029 dB (Class B)
Expressed in relative uncertainty: 
10 -3 ; degrees of freedom v 17 =v 11 =2
The effect of the attenuator, its standard uncertainty: u 18 =u 12 =0.167 dB (Class B)
Expressed in relative uncertainty: 
10 -2 ; its value is stable, and the degree of freedom v 18 =∞.
Synthetic standard uncertainty:
At this point, the uncertainty of the various factors affecting the attenuation is:
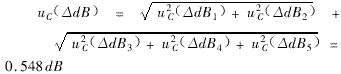
2.2 Thickness effect
The average value of 100 measurements was 100, the standard deviation s=0.15 mm, standard uncertainty:
Expressed in relative uncertainty: u' 19 = 4.74 × -4 ; degree of freedom v 19 = 10-1 = 9
The caliper minimum reading is 0.02, the error is subject to uniform distribution, the distribution range (-0.01, +0.01), its standard uncertainty:
Expressed in relative uncertainty: u' 20 = 5.8 × 10 -5 ; degree of freedom v 20 = (50%) -2 = 2
The caliper uncertainty is 0.05 (k=3), subject to normal distribution, standard uncertainty:
Expressed in relative uncertainty: 
10 -4 ; its value is stable, and the degree of freedom v 21 =∞.
The standard uncertainty of workpiece thickness synthesis is synthesized by the above three items, namely:
2.3 defect equivalent size
Transfer Function:
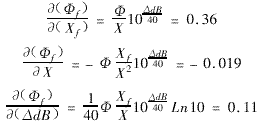
Synthetic standard uncertainty:
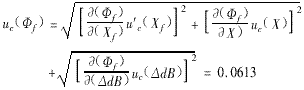
Expressed in relative uncertainty: u' c (Φ) = 3.08 × 10 -2
Effective degrees of freedom:
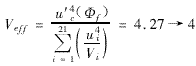
The confidence level is 95%, then the coverage factor: t P (4) = 2.78
U=t P . u c (Φ f )=2.78×0.0613=0.17
The final result of the equivalent size is Φ f =1.99±0.17 mm (0.17 mm is the measurement uncertainty of the test results)
3 Conclusion
Through the calculation and evaluation of the measurement uncertainty of the quantitative analysis of longitudinal wave flaw detection, the reliability degree of the quantitative analysis results of the flaw detection can be known, and the error source of the test process and the result analysis and the influence degree of the joint test result can be determined. The evaluation of measurement uncertainty is an important part of the test results and can be applied to various fields of quantitative analysis of non-destructive testing.
About the author: Wu Jianping, male, born in 1962, engineer
Author: Wu Jianping (Jiangling Motor Co., Ltd., Nanchang 330001, China)
Wei Zhihua (Jiangling Motor Co., Ltd., Nanchang 330001, China)
references
[1] BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML, Guide to the Expression of Uncertainty in Measurement, ISO, 1995;
[2] Xia Jizhen, Acoustic Nondestructive Testing Technology, Nanchang: Nanchang Institute of Aeronautical Industry, 1991;
[3] Liu Zhimin, Evaluation of Measurement Uncertainty, Beijing: China Institute of Technical Supervision and Information, 1995;
[4] Editor-in-Chief Chen Yuqin, Application Example of Measurement Uncertainty "93 International Guide", Beijing: China Metrology Press, 1998.
Digital Water Curtain Fountain
We are a modern enterprise specializing in the production and sales of indoor and outdoor fountains and other products. We have a design and construction team with nearly 30 years of experience.Our company mainly engages in various kinds of music fountains, light shows, digital water curtains, water curtain movies, dry sprays and other diversified fountains.Digital water curtain not only gives people a supernatural enjoyment of the trinity of sound, shape and color, but also takes water as the basic element. It is a new type of waterscape equipment with a sense of science and technology.
Digital Water Curtain Fountain,Water Screen Fountain,Fountain Outdoor,Digital Water Curtain Fountain
Wuxi Jinshanghua Environmental Equipment Co., Ltd , https://www.jshfountain.com